Lesson 2 Syntax, arithmetic, & nesting

AutoLISP programs are made up of a series of expressions, each of which accomplishes a small step in the overall task.  In general, an expression will have a form similar to this:

        ( function   first-argument   second-argument   etc....  )

Here is one of the expressions from line 5 of the sample program in Lesson 1.

    (/ w 2)    This expression would be read "divide w by 2."

The syntax (form) of the above expression can be described as follows:

• The expression is a list, that is, it begins with an opening parenthesis and ends with a closing parenthesis.  Every AutoLISP expression is a list.
• The function (the forward slash, which is the symbol for division) is the first element in the list.  Functions are always placed at the beginning of the list.  (This is known as prefix notation.)  The function can also be called the operator, and the arguments can be called the operands.
• After the function there are two arguments:  the variable w and the number 2.  Most functions have one or more arguments, but some functions have no arguments.

Based on the above syntax, the AutoLISP interpreter has a relatively easy job whenever an expression is sent to it.  Once the interpreter looks at the first element (the function), it knows exactly what to do with the remaining elements (the arguments).

Expressions are sent to the AutoLISP interpreter in several ways.  One way is to type the expression at the AutoCAD command prompt.  When the AutoCAD command interpreter sees that the first character is an opening parenthesis, it submits the expression to the AutoLISP interpreter, which evaluates (or, executes) the function and returns its value.

Other ways to send expressions to the AutoLISP interpreter include loading  files that contain AutoLISP expressions and selecting menu items that include AutoLISP expressions.  These methods are discussed in later lessons.  For the remainder of this lesson we will limit ourselves to typing expressions at the command prompt.

How you type an expression is important.

• Put a space after the function.  If you forget this space, the AutoLISP interpreter will continue reading until it finds a space and think that you have called for a function with a longer name.
• Put a space between each argument.
• Don't forget the closing parenthesis  If you do, AutoLISP will display a message that looks like this "1>" to remind you to type in one closing parenthesis.  To complete the expression and get back to the command prompt, type the missing parenthesis.  (If you are typing nested expressions and forget several closing parentheses, the message will include the number of parentheses you are lacking.)
• If you enter decimal fractions, such as .25, you must type them with a leading zero (0.25), otherwise AutoLISP will consider your fraction an invalid dotted pair (more about dotted pairs later).

Here are some expressions to type in at the AutoCAD command prompt.  Type them exactly as they are shown.  For now we will limit ourselves to the four basic arithmetic functions of addition, subtraction, multiplication, and division, and the math function of square root.  Under each heading is an explanation of the function.

If you really want to master AutoLISP, pay attention to this tip:  Don't limit your practice to the expressions listed here or in other lessons.  Make up many expressions of your own.  As you try each of your own expressions, predict its results.  Before you enter the closing parenthesis, figure out what you think the result should be.  When you get really good at predicting the results, you will know that you are analyzing the expression the same way the AutoLISP interpreter analyzes it, and that means you understand the expression's syntax and how it is interpreted.  This approach will become especially helpful when you get to more complex functions later.

By the way, integers used in AutoLISP can range from negative two billion to positive two billion (actually from -2,147,483,648 to +2,147,483,647).

Addition (+)

This function adds all arguments, paying attention to signed numbers.  Positive numbers can be entered with or without the plus sign.  The function will usually have two or more arguments.  If only integers are added, an integer is returned.  If one or more of the arguments is a real (a "floating point" decimal number), then a real is returned.  You can have one, two, or several arguments.  Although the function must be first, the arguments can be in any order and still give the same result.

(+ 10 5)

returns 15

(+ 10 -5)

returns 5

(+ -10 5 3)

returns -2

(+ 10.5 4.5)

returns 15.0

(+ 10.0 4)

returns 14.0

(+ 8 7 6 5)

returns 26

(+ 8)

returns 8

(+ 5 10 15

returns the message "1>".  Type in the missing closing parenthesis to complete the expression.

(+3 4 5)

returns the message "error: bad function" because there is no space after the function.  (The "+3" is interpreted as a positive 3, and there is no function named 3.)  Notice the code that is dumped to screen after the error message.

(+ 1.75 .25)

returns the message "invalid dotted pair" because the zero is missing in front of the .25.  Try it again with the zero in place.

Subtraction (-)

This function starts with the first argument and subtracts each subsequent argument from it.  It pays attention to signed numbers.  One or more reals means the result will be real.  The function will usually have two or more arguments.  The function must be first, then the first argument, but all arguments after the first argument can be in any order.  (In effect, the sum of all the arguments after the first argument is subtracted from the first argument.)

(- 10 5)

returns 5

(- 5 10)

returns -5

(- 10 5 3)

returns 2

(- 20 -5)

returns 25

(- 30 15 14 13)

returns -12

(- 10 6.25)

returns 3.75

(- 10)

returns -10   When there is only one argument to the subtract function, it does not follow its usual procedure.  Rather than subtracting nothing from 10, it subtracted 10 from 0 to get the negative 10!  We will be able to use this later to change the sign of a number or a variable.

Multiplication (*)

All arguments are multiplied, paying attention to signed numbers.  One or more reals means the result will be real.  The function will usually have two or more arguments.  Although the function must be first, the arguments can be in any order and still give the same result.

(* 3 4)

returns 12

(* 3 -5)

returns -15

(* 2 4 6 8)

returns 384

(* 2 4.5)

returns 9.0

(* -5 -6)

returns 30

(* 1.0625 2.375)

returns 2.52344    If you multiply these two numbers by hand or with a calculator, you will see that the correct answer has eight significant digits (2.5234375) rather than six as displayed by AutoLISP.  However, when AutoLISP displays such a number it always rounds it to six significant digits.  AutoLISP is much more accurate than six significant digits.  In fact, it is accurate to between 14 and 17 significant digits.  It is only when it gives its default display of such a number that it does this rounding.  If the above multiplication were done in a program, the result would be accurate well beyond the required eight significant digits.  You can prove this by entering  (rtos (* 1.0625 2.375) 2 14) which forces AutoLISP to display more digits.  The rtos function will be discussed later.  See the "NOTE REGARDING ACCURACY" at the beginning of "6 - Arithmetic tests."

Division (/)

This function starts with the first argument and divides it by the second, then divides that quotient by the third, etc.  It pays attention to signed numbers.  One or more reals means the result will be real.  The function will usually have two or more arguments.  The function must be first, then the first argument, but all arguments after the first argument can be in any order.  (In effect, the first argument is divided by the product of all the arguments after the first argument.)   IMPORTANT: If all arguments are integers, then the type of division that is performed is integer division, which ignores any remainder, as you will see from the examples.
 

(/ 10 2)

returns 5

(/ 10.0 2)

returns 5.0

(/ 6 -2)

returns -3

(/ 10 3)

returns 3    This is integer division; the remainder of 1 is discarded.

(/ 10 3.0)

returns 3.33333    Since the 3.0 is a real, real (floating point) division is performed rather than integer division.

(/ 100 10 2)

returns 5

(/ 100 10.0 4 10)

returns 0.25

Square root (sqrt)

This function takes one argument, either a real or an integer, and returns the square root as a real.

(sqrt 9)

returns 3.0

(sqrt 2.00)

returns 1.41421

(sqrt -4.00)

returns the message "function undefined for argument" because of the negative 4

Expressions are often nested.  That is, one list is placed inside another.  Here is an expression that illustrates nesting from line 12 of the sample program in Lesson 1.

  (setq ang (angle a b))

The inner expression (angle a b) is executed to obtain the angle between point a and point b.  The angle that is shown in the illustration in Lesson 1 is approx. 20°, so we will use that angle for our discussion.  But the angle function returns its answer in radians, so it would return 0.35.  Since 0.35 is the value of the inner expression, you could say that the outer expression boils down to (setq ang 0.35) after the inner expression has been evaluated.

When you want to analyze a nested function, always evaluate the innermost expression first, then work your way out to the larger expressions, no matter how many levels of nesting are involved.

All nested expressions which are on the same level, such as the two inner expressions in the following example, are evaluated left to right.

   (* (+ 4 5) (- 11 8))

Actually, the above description is not completely correct.  It describes the way we humans evaluate nested expressions.  But AutoLISP, being much more simple minded than we, uses a different procedure to arrive at the same answer.  AutoLISP begins reading the expression from the left and tries to evaluate it as far as it can.  Each time it runs into another opening parenthesis, it sets its current information aside on a stack to be retrieved later.  This may happen many times as it encounters more and more nested expressions.  When it finally reaches an expression which does not contain any more nested expressions, it is able to complete its evaluation of that expression and then use that value to complete the evaluation of the next outer expression, and so forth, until it has recovered all its information from the stack and evaluated all expressions.   Even this rather wordy explanation would be an oversimplification for some complex expressions.  Nevertheless, the important point is that the result is the same when AutoLISP uses its stacking procedure and when we use our procedure of finding the innermost expressions and evaluating them first.  For that reason, we will at times ascribe our procedure to the AutoLISP interpreter just to simplify the discussion.

When you know the order of operations required to solve an algebraic expression, you can write an equivalent AutoLISP expression, which will nearly always involve nested expressions.  For example, consider the formula for the perimeter of a rectangle:

      2(length + width)

In this formula, first the length and width are added, then that sum is multiplied by 2.  The equivalent AutoLISP expression is shown below.  (The variables have been shortened for reasons that are explained in the next lesson.)

  (* 2 (+ len wid))

The AutoLISP interpreter evaluates the inner expression first, then that sum is multiplied by 2 to arrive at the same results as the algebraic formula.

The program name, area3, stands for "area of triangle when 3 sides are known."

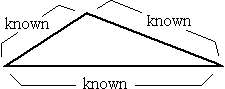
This program is a good illustration of all four of the functions covered in the lesson, plus a few additional functions.

The formula is the well known two step formula which first calculates the intermediate value S, which is half the sum of the sides.

      S = (a + b + c) / 2

Then S is used to calculate the area, which is the square root of the product of S, S - a, S - b, and S - c.

      Area =  (S (S - a) (S - b) (S - c))^½

In an attempt to keep the program simple, it does not check for invalid triangles (such as one with sides that are 5, 5, and 11).  If these numbers were entered as the lengths of the sides, the program would crash since it would produce a negative number for the square root function.  Also, it does not have an error routine.  It would also be nice to have the program calculate all three angles, but that requires the use of the trig functions which will be covered later.

Notice the use of the various arithmetic functions in nested expressions.  Also notice how the program translates the algebraic notation of the two formulas above into AutoLISP expressions.  There are more samples of translated formulas in the next lesson.

The program can be understood in three sections.

• Input,   Lines 2-4
• Calculate,   Lines 5-7
• Report,   Lines 8-11

------ marker ------ beginning of working program ------ try it out ------

;| AREA3, short for AREA of triangle when 3 sides are known.
   Copyright © 1998 Ronald W. Leigh
Variables:
a     Side a
area  Area of triangle
b     Side b
c     Side c
p     Perimeter
s     Intermediate value          |;

(defun c:area3 (/ a area b c p s)                 ;line  1
(setq a (getreal "\nLength of side a: "))         ;line  2
(setq b (getreal "\nLength of side b: "))         ;line  3
(setq c (getreal "\nLength of side c: "))         ;line  4
(setq p (+ a b c))                                ;line  5
(setq s (/ p 2))                                  ;line  6
(setq area (sqrt (* s (- s a) (- s b) (- s c))))  ;line  7
(princ "\nThe area is ")                          ;line  8
(princ area)                                      ;line  9
(princ "\nThe perimeter is ")                     ;line 10
(princ p)                                         ;line 11
(princ)                                           ;line 12
)                                                 ;line 13

-------- marker -------- end of working program -------- try it out --------