Lesson 6 Geometry & Command Functions

AutoLISP includes a set of functions that work with the geometry of your drawing or model.  These functions can both extract information from known locations and calculate new locations (see "2 - Geometry and trigonometry" in the "Catalog of function definitions").  The geometry functions often work side by side with the command function (see command in "14 - Working with AutoCAD" in the "Catalog of function definitions").

This section describes three geometry functions that you will use in many of your programs: distance, angle, and polar.  The distance and angle functions are similar, so they are described together.  Polar is the main function for generating new points based on known points.

Another function which can be helpful in certain circumstances is inters (short for intersect).  Its use is rather straightforward so it is not described below (see inters in "2 - Geometry and trigonometry" in the "Catalog of function definitions").

Distance and angle

Often your program needs to find the distance and/or angle between two given points.  The two functions distance and angle accomplish this.  Both functions have the same syntax; they take two points as arguments.  For example, given the two points p1 and p2, typical usage of these two functions might look like this:

    (setq dis (distance p1 p2))
    (setq ang (angle p1 p2))

The distance function returns a real number which is the distance between the two points.  Either point can be cited first.  In other words, both (distance p1 p2) and (distance p2 p1) return the same distance.  Also, the two points can be at different Z levels, in which case the actual 3D distance between them in space is returned.  (Compare the angle function described next.)

The angle function returns a real number which is the radian measure of the angle from the first point to the second.  The angle is measured from the Cartesian zero angle (3 o'clock).  Unlike the distance function, the order to the two points is important.  Reversing the two points results in answers that differ by π radians (180°).  In other words, if p1 is at 1,1,0 and p2 is at 2,2,0,

    (angle p1 p2) returns 0.785398 radians, that is, 45°
    (angle p2 p1) returns 3.92699 radians (3.14159 + 0.785398), that is, 225° (180° + 45°)

The angle function always returns a positive angle between 0 and 2π (360°).  Also, the two points can be at different Z levels, but the Z levels of the points are ignored.  In effect, the two points are projected onto the current X-Y construction plane for the calculation of the angle.

Don't confuse the distance function with either the DIST command (which allows the user to pick two points and reports the 3D distance between them as well as delta-x, delta-y, and delta-z), or with the DISTANCE system variable (which holds the most recent distance reported by the DIST command).

Occasionally new AutoLISP programmers confuse distance with getdist, and angle with getangle.  The two get-functions pause for user input, but the distance and angle functions do not pause.

Polar

The polar function is a workhorse, which you will use over and over again in your programs.  It is also one of the more complex functions covered so far, taking three arguments whose order is critical.  So it is well worth your while to study the polar function carefully.

The polar function returns a new point (a list of three reals) based on three things:

• a base point
• the angle from the base point (the angle is in radians)
• the distance from the base point

    (polar (list 2 4 0) 1.04 5.25)

The above expression instructs AutoLISP to start at 2,4,0 (the base point), proceed along angle 1.04 radians for a distance of 5.25, and return the coordinates of that point, (which happen to be 4.65766,8.52762,0.0).

The first argument is the known point.  The second argument is an angle in radians.  The third argument is the distance.  These three arguments must be given in this order.  (Notice that polar expects the angle before the distance.  Even though it is called "polar," it differs from "polar coordinates" in which you enter the distance before the angle, such as @5<30.)

The polar function always returns a point that is in the same X-Y construction plane (that is, at the same Z level) as the base point.

Distance and angle

We will work with the four corners of a 1 unit square.  Place four points, LL (lower left), LR (lower right), UL (upper left), and UR (upper right), in variables by typing the following:

    (setq LL (list 4 4 0) LR (list 5 4 0) UL (list 4 5 0) UR (list 5 5 0 ))

Notice that, contrary to custom, we are using upper case variable names because the lower case letter "l" and the number "1" are easily confused.

Use the distance and angle functions to get the distance and angle from each point to the other three.  For example, starting with the LL corner:

    (distance LL LR)  returns 1.0
    (angle LL LR)  returns 0.0

    (distance LL UR)  returns 1.41421
    (angle LL UR)  returns 0.785398

    (distance LL UL)  returns 1.0
    (angle LL UL)  returns 1.5708

Do the same starting with the other corners.  Notice that the distances are always positive, the angles are always positive, and both distances and angles are always returned as reals.

Also experiment with points that are not on the same Z level.

Polar

First enter (setq a (list 3 3) b (list 6 6)).  Then enter the following expressions, plus several of your own.  Important:  predict the results of the polar functions before you press 'Enter'.  When you can estimate the results consistently you know you understand the polar function.

(polar a 0 2)
(polar a (/ pi 2) 2)
(polar a -0.785 1)
(polar b pi 2)
(polar b (* pi 1.5) 2)
(polar b (* pi 1.25) 3)

The command function allows the AutoLISP interpreter to submit instructions to the AutoCAD command interpreter.  The arguments for the command function are the name of the AutoCAD command and the appropriate responses, that is, the AutoLISP expression must submit information to the AutoCAD command in the same order as you would if you were running the command from the keyboard.

For example, if your program needs to draw a circle located at 5,3 with a radius of 1.25, the expression would look like this:

    (command ".circle" (list 5 3) 1.25)

The dot before the command name insures that the built-in command will be used.  This avoids your program mistakenly using a command called circle which has been altered by the user or by another AutoLISP program.  (Methods of altering AutoCAD commands are covered in a later lesson.)

By default, the circle command prompts for the center of the circle then the radius, so the above expression is appropriate for those default prompts.  However, you may prefer to submit the diameter rather than the radius, in which case your expression would look like this:

    (command ".circle" (list 5 3) "D" 2.5)

Or, perhaps you need to create a "2 point" circle (indicating the two endpoints of a diameter).  Then your expression might look like this:

    (command ".circle" "2P" (list 1 8) (list 1 7))

Notice that responses to options, such as the "D" for diameter and the "2P" for a 2-point circle are enclosed in quotation marks.

Some commands require the user to press 'Enter' in order to exit the command and return to the command prompt.  For example, the LINE command continues to prompt for the next point until the user presses 'Enter'.  Thus in order to complete the command, your expression must include a null string at the end, like so:

    (command ".line" (list 12 10) (list 8 10) (list 8 6) (list 4 6) "")

The above expression draws three line segments between the four points, then exits the LINE command.

Sometimes you want your program to supply some of the input for the AutoCAD command, but you need to user to enter information at certain points.  You can use pause (no quotation marks, it is a pre-assigned variable) as illustrated below.

    (command ".donut" 0.5 0.75 pause "")

The above expression runs the DONUT command, sets the inside diameter at .5 and the outside diameter at .75, then pauses for the user to indicate the location of the center.  The user can pick the center point with the mouse or can enter coordinates from the keyboard.  The DONUT command keeps prompting, so the final null string ("") is needed to exit the command.  Immediate osnaps and filters can also be introduced by the user during the pause.

Figuring out the prompt sequence

For most commands you can simply run the command from the keyboard to see its prompt sequence and its keyword options.  The sequence needed in the AutoLISP expression is exactly the same as that needed at the keyboard.

But what about commands that bring up a dialog box, such as the PLOT and OPEN commands?  If you set system variables CMDDIA and FILEDIA to 0, then you will get the command-line version of these commands and can study their sequence of prompts.

However, there are some commands that bring up a dialog box even when CMDDIA and FILEDIA are both set to 0, such as the LAYER command.  In this case, simply start the command-line version of the command with an expression like this:

    (command ".layer")

Then you will be able to complete the command from the keyboard and determine the sequence.

Run the following commands by writing AutoLISP expressions using the command function.  The first five commands are completed for you.

1. Create a .75 diameter circle at 2,2.

(command ".circle" (list 2 2) "D" 0.75)

2. Create a circle that goes through 3,3   4,3   and   4,4.

(command ".circle" "3P" (list 3 3) (list 4 3) (list 4 4))

3. Move the last entity one unit to the left.

(command ".move" "L" "" (list 1 0) (list 0 0))

4. Create three concentric circles at 2,6 with radii of .5, .7, and .9.

(command ".circle" (list 2 6) 0.5 ".circle" (list 2 6) 0.7 ".circle" (list 2 6) 0.9)

5. Create a 1.5 unit square with its lower left corner at 6,6 using the LINE command.

(command ".line" (list 6 6) (list 7.5 6) (list 7.5 7.5) (list 6 7.5) "C")

6. Create a 1.5 unit square with its lower left corner at 4,6 using the PLINE command.

7. Erase the last square.

8. Move all the circles up one unit.

9. Zoom in on the right half of the screen.

10. Stretch the square so it is 3 units wide.

11. Create a new layer and make it current.

12. Setup: set PDMODE to 34 and draw a diagonal line on screen.  Then write an AutoLISP expression that divides the line into 11 segments (pause to let the user select the line).

13. Setup: create a block.  Then write an AutoLISP expression which inserts the block at full scale and at zero rotation (pause to let the user pick the insertion point).

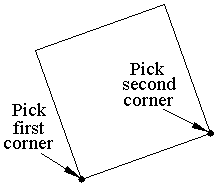
This program draws a square at any angle by getting two points from the user.  It does not do anything that cannot also be done using the Edge option of the POLYGON command, but it is an easy to understand example of all the functions covered in this lesson.

------ marker ------ beginning of working program ------ try it out ------

;|  SQUANGLE, short for SQUare at any ANGLE
    Copyright © 1988 Ronald W. Leigh
    Input: User picks two points anywhere on screen
    Output: Program draws square using the two points
     as the first two corners
Variables:
ang          Angle of first side
len          Length of side
p1/p2/p3/p4  Corners of square            |;

(defun c:squangle (/ ang len p1 p2 p3 p4)
(initget 1)
(setq p1 (getpoint "\nFirst corner of square: "))
(initget 1)
(setq p2 (getpoint p1 "\nSecond corner of square: "))
(setq len (distance p1 p2) ang (angle p1 p2))
(setq p3 (polar p2 (+ ang (/ pi 2)) len))
(setq p4 (polar p1 (+ ang (/ pi 2)) len))
(setvar "cmdecho" 0)
(command ".pline" p1 p2 p3 p4 "C")
(setvar "cmdecho" 1)
(princ)
)

------- marker ------- end of working program ------- try it out -------

This program draws a circular pattern of holes that are equally spaced around a center point in what is typically called a bolt circle.

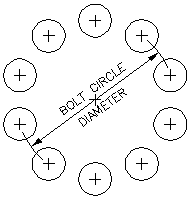
Although the same thing can be accomplished fairly easily with the CIRCLE and ARRAY commands, this program streamlines that procedure somewhat, and provides a good example of the use of the polar and command functions.  Beginning in line 14 there is a repeat function, which is explained in a later lesson.

------ marker ------ beginning of working program ------ try it out ------

;|  BOLTCIRC, Bolt Circle
    Copyright © 1998 Ronald W. Leigh
    Draws a circular pattern of holes
    equally spaced around a center point
Input: Center of bolt circle, diameter of bolt circle,
       number of holes, diameter of holes
Output: Draws circular pattern of holes plus centerline

Variables:
ang     Angle from center of bolt circle to each hole
anginc  Angle between subsequent holes
bcdia   Bolt circle diameter
cp      Center of bolt circle
hdia    Hole diameter
leg     Centerline leg length
loc     Center location of each hole
num     Number of holes                   |;

(defun c:boltcirc (/ ang anginc bcdia cp hdia leg loc num)
(setq pi 3.1415926535897932385)
(setq cp (getpoint "\nCenter of bolt circle: "))
(setq bcdia (getreal "\nBolt circle diameter: "))
(setq num (getint "\nNumber of holes: "))
(setq hdia (getreal "\nDiameter of each hole: "))
(setq ang (/ pi 2) anginc (/ (* 2 pi) num))
(setq leg (/ hdia 6))
(setvar "cmdecho" 0)
(command ".line"
  (polar cp pi leg) (polar cp 0 leg) "")
(command ".line"
  (polar cp (* 1.5 pi) leg) (polar cp (* 0.5 pi) leg) "")
(repeat num
  (setq loc (polar cp ang (/ bcdia 2)))
  (command ".circle" loc "D" hdia)
  (command ".line" (polar loc pi leg)
                   (polar loc 0 leg) "")
  (command ".line" (polar loc (* 1.5 pi) leg)
                   (polar loc (* 0.5 pi) leg) "")
  (setq ang (+ ang anginc)))
(setvar "cmdecho" 1)
(princ))

------- marker ------- end of working program ------- try it out -------

This program draws the type of numbered balloon which is typically used in an assembly drawing to point to parts described in a stock list or bill of materials.

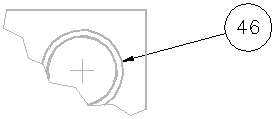
Balloon is a more realistic and usable program than the previous one, and it includes several additional examples of the command function.  There are several aspects of this program which are explained below.  The program also has several occurrences of the if function, which is explained in a later lesson.

Saving the user's osnap mode

In section 10, the current setting of system variable osmode (osnap mode) is stored in variable oom so it can be restored at the end of the program, section 40.  In section 20, osmode is set to 512 (nearest) while the user picks the "Startpoint of arrow,"  then set to 0 until the end of the program.

The balloon number (blnnum) default -- section 20, last 5 lines

Balloons are often drawn in sequence, so it makes sense to offer number 1 as the default the first time the program is run, and increment this default by one each time the program is re-run.

These five program lines begin by checking to see if variable blnnum is nil.  If blnnum is nil, then blnnum is set to zero in preparation for being incremented in the next line.  (In a more sophisticated program, the global variables will not only be checked to see if they are nil, but their type and range will also be checked.)

The prompt is a concatenated string which includes the default balloon number (converted from an integer to a string so it can be joined to the rest of the prompt string).  If the user presses 'Enter' in response to this prompt, nil is assigned to variable temp.  Thus, in the next line, blnnum is not reset.  But if the user enters a number, that number is assigned to variable temp which, in the next line, is also assigned to blnnum.

Notice that blnnum is a global variable.  It is marked "GLOBAL" in the documentation and, more importantly, it is omitted from the list of variables in the first line of the program.  Thus, blnnum holds its value after the program is finished.

The program would run fine if this variable name had been num.  But since it is a global variable, it is better to extend the name so it is unique to this program.  If you have two programs both using global variables with the same name, one program might set the variable to a value which causes the other program to crash.

The balloon diameter (blndia) default -- section 20, first 9 lines

This program maintains a fixed ratio (7/25 or .28) between the height of the text inside the balloon and the diameter of the balloon in order to allow 3-digit numbers to fit inside the balloon.  Notice that, at the end of section 30, the program sets the text height at .28 times the balloon diameter.  The program does not allow the user to set the text height independently of the balloon diameter (except in the case of a text style with a fixed height, which is discussed below).

When getting the balloon diameter near the beginning of section 20, the program must calculate a default diameter that is reasonable for the current drawing settings (the dimensioning text height from system variable DIMTXT and the current setting of the dimensioning scale from system variable DIMSCALE, with the .28 factor included).  This is done by the nested if expressions at the beginning of section 20.  The first time the program is run, variable blndia is nil so line 1 in this section forces a calculation.  Then the second line checks the value in DIMSCALE to determine which of two possible calculations should be performed.  If the user has set DIMSCALE to zero (which is often done when using paper space viewports) the calculation does not use DIMSCALE as one of its factors.

If the user accepts this calculated default, the text in the balloon will be the same height as the text in the dimensions.  However, in many drawings, balloon text is larger than dimension text, so the user may want to enter a slightly larger value when prompted for the balloon diameter.  After the user has determined a balloon diameter, either by accepting the default or by entering a number, that same diameter is offered as a default the next time the program is run.

Drawing the leader -- section 30, line 6

There are two ways to create leaders in AutoCAD.  One is to use the LEADER command at the command prompt.  The other is to enter dimensioning mode by entering DIM or DIM1, then enter LEAder.  This program uses the second method, which allows the creation of the arrowhead and line, then an 'escape' which cancels the rest of the command.  The 'escape' is caused by using the command function with no arguments (command).  The first method cannot be used because it deletes the arrowhead and line when 'escape' is used.

The text command and fixed-height text -- section 30

This is the same problem we encountered in the sample program in the previous lesson in connection with the text used as a header for the table.  If the current text style has a fixed height (that is, its height setting is greater than zero), then the text command does not prompt for height as it would otherwise.

The program gets the name of the current text style in the second line in this section, placing it in variable ts.  Then in the third line, it uses the tblsearch function to get the height setting, placing it in variable tshei.  (The tblsearch function is explained in a later lesson.)  Then, in the last four lines, an if function evaluates variable tshei.  If tshei is greater than zero (which indicates a fixed height) then the text command is run without indicating any height.  If tshei is zero, then the text command is run and height is included.

Since text with a fixed height may not fit properly in the balloon, line 4 of this section gives the user a message explaining the situation.

Enhancements to this program

This program is expanded in later lessons.  In Lesson 12 on Files, you will find a revision of this program called balloon2.lsp, which stores the balloon diameter in a file so that it can appear as the default diameter across editing sessions.  And in Lesson 14 on Table Access, you will find a revision of the balloon2.lsp program called balloon3.lsp, which accesses the layer table in order to switch to (or create, if needed) a layer on which to place the balloons.  Balloon3.lsp also contains a separate setup routine so the user does not have to constantly "click through" the defaults each time the program is run.

Reminder:  This program contains some lines that are longer than previous sample programs.  To view the program's format properly, make sure you have maximized your browser window.

------ marker ------ beginning of working program ------ try it out ------

;|  BALLOON
    Copyright © 1988,1998 Ronald W. Leigh
    Input: size of balloon, arrow location,
           balloon location, size of balloon, number
    Output: draws assembly balloon
Variables:
blndia  Balloon diameter, GLOBAL
blnnum  Balloon number, GLOBAL
cen     Center of balloon
ep      Endpoint of arrow
oom     Old osnap mode
sp      Start point of arrow
temp    Temp. value for blndia and blnnum input
ts      Name of current text style
tshei   Text style height                              |;

;10====PROGRAM SETUP

(defun c:balloon (/ cen ep oom sp temp ts tshei)
(setq oom (getvar "osmode"))
(graphscr)

;20====GET SIZE, START POINT, CENTER, & NUMBER

(if (null blndia)
  (if (= 0 (getvar "dimscale"))
    (setq blndia (/ (getvar "dimtxt") 0.28))
    (setq blndia (/ (* (getvar "dimtxt") (getvar "dimscale")) 0.28))
  )
)
(initget 6)
(setq temp (getreal (strcat "\nBalloon diameter <" (rtos blndia 2 3) ">: ")))
(if temp (setq blndia temp))

(setvar "osmode" 512)
(initget 1)
(setq sp (getpoint "\nStartpoint of arrow: "))
(setvar "osmode" 0)

(initget 1)
(setq cen (getpoint sp "\nLocation of balloon: "))

(if (null blnnum) (setq blnnum 0))
(setq blnnum (1+ blnnum))
(initget 6)
(setq temp (getint (strcat "\nBalloon number <" (itoa blnnum) ">: ")))
(if temp (setq blnnum temp))

;30====CALCULATE END POINT OF ARROW, GET TEXT STYLE HEIGHT, DRAW BALLOON

(setq ep (polar cen (angle cen sp) (/ blndia 2)))

(setq ts (getvar "textstyle"))
(setq tshei (cdr (assoc 40 (tblsearch "style" ts))))
(if (> tshei 0) (princ "\nText style has fixed height; may not fit balloon."))

(setvar "cmdecho" 0)
(command ".dim1" "leader" sp ep) (command)
(command ".circle" cen "D" blndia)

(if (> tshei 0)
  (command ".text" "M" cen 0 blnnum)
  (command ".text" "M" cen (* 0.28 blndia) 0 blnnum)
)

;40====RESET

(setvar "cmdecho" 1)
(setvar "osmode" oom)
(princ)
)

------- marker ------- end of working program ------- try it out -------