Lesson 7 Trig Functions

AutoLISP includes only three trigonometric functions:

• sin,   short for sine
• cos,  short for cosine
• atan,   short for arc tangent

The sin and cos functions each take a single argument, which is an angle in radians.  See radian in the Glossary.  For example, given the fact that π/6 = 30°, π/4 = 45°, π/3 = 60°, and 2π/3 = 120°

    (sin (/ pi 6))  returns 0.5
    (sin (/ pi 4))  returns 0.707107
    (sin (/ pi 3))  returns 0.866025

    (cos (/ pi 6))  returns 0.866025
    (cos (/ pi 4))  returns 0.707107
    (cos (/ pi 3))  returns 0.5
    (cos (* 2 (/ pi 3)))  returns -0.5

Defining your own tangent function

Since AutoLISP has no built-in tangent function, you have to define your own, as follows:

    (defun tan (ang) (/ (sin ang) (cos ang)))

When you have a program than needs a tangent function, you can add the above definition to the program file and it will be loaded into memory when the program is loaded and thus be available for the program to use.

The arc tangent is the opposite of the tangent.  The tangent function accepts an angle (in radians) and returns a ratio -- the ratio of the opposite side to the adjacent side, which is the same as the ratio of the sine to the cosine.  In contrast, the arc tangent function accepts the ratio and returns the corresponding angle (in radians).

The atan function accepts the ratio by accepting either one or two arguments.  When only one argument is used, the atan function returns values in a limited range (from -π/2 to +π/2, that is, from -90° to +90°, or quadrants I and IV).  But when two arguments are used, it can return any angle in a full circle.  (See atan under "2 - Geometry & Trigonometry" in the "Catalog of function definitions".)

When only one argument is used, that argument can be either positive or negative, and the angle that is returned is limited to quadrants I and IV as illustrated below.

    (atan 1.0)  returns 0.785398  (the radian equivalent of 45°, in quadrant I)
    (atan -0.2)  returns -0.197396  (the radian equivalent of -11.31°, in quadrant IV)

But when two arguments are used, both arguments can be either positive or negative, which yields four possible combinations of positive and negative arguments, which allows atan to return angles in all four quadrants as illustrated below.

    (atan 2.5 2.5)  returns 0.785398  (angle is in quadrant I)
    (atan 2.5 -3.0)  returns 2.44685  (angle is in quadrant II)
    (atan -4.5 -5.0)  returns -2.40878  (angle is in quadrant III)
    (atan -3.0 2.5)  returns -0.876058  (angle is in quadrant IV)

The atan function divides the first argument by the second to determine the ratio.  It also uses the signs of both numbers to determine the quadrant and thus the size of the angle.  The sign of the angle that is returned is always the same as the sign of the first number.

When atan divides the first argument by the second, it floats the arguments in order to avoid integer division.  Consider the following two examples.

    Correct:    (atan 18 -13)  returns 2.19628 (= 125.84°)
    Incorrect:  (atan (/ 18 -13))  returns -0.785398 (= -45°)

Some beginning AutoLISP programmers are tempted to divide the two numbers before submitting them to the atan function, as shown in the "incorrect" example above.  But the result is incorrect on two accounts:  First, the quotient of positive 18 and negative 13 is negative, and when a single negative argument is submitted to atan, a negative angle is returned.  Second, submitting 18 and -13 to the divide function yields -1 because of integer division, but the atan function promotes both integers to reals and calculates the correct quotient.  Thus, using the "incorrect" approach produces an angle that is incorrect both in magnitude and sign.  When you know the vertical and horizontal vectors, it is better to submit them as two separate arguments to the atan function.

Suppose you are writing a program which knows the sine or cosine of an angle and needs to find the angle.  Your program can use the Pythagorean theorem (c² = a² + b²).  When the hypotenuse is 1 and the two legs of the right triangle represent the sine and the cosine as shown in the diagram above, the pythagorean theorem can be reduced to

      cosine = ±(1 - sine²)½      --or--      sine = ±(1 - cosine²)½

So, if your program knows the sine, it can calculate the cosine, and vice versa.  Then it can submit both sine and cosine to the atan function to yield the angle.  But remember the plus-or-minus sign in the above formulas.  This introduces some ambiguity into your program, which may have to use the atan function twice (once with the positive, once with the negative) for a complete solution.

The above discussion correlates with the nature of the tangent function itself.  Two angles can have the same tangent.  For example, 150° and -30° both have a tangent of -0.57735, and 45° and -135° both have a tangent of 1.00.  (The two angles that have the same tangent are always 180° apart.)  So your program may have to take both angles into account.

Since AutoLISP has no arc sine or arc cosine functions, you can define your own functions as shown below using the formulas discussed above.  These definitions are subject to the same ambiguity described above.

    (defun asin (sine) (atan sine (sqrt (- 1 (* sine sine)))))

    (defun acos (cosine) (atan (sqrt (- 1 (* cosine cosine))) cosine))

Both of the above definitions use the positive root, therefore the asin function only returns angles in quadrants I and IV, and the acos function only returns angles in quadrants I and II.  In each case your program may have to evaluate the other angle (180° larger or smaller) for a complete solution.

Use all three built-in trig functions, sin, cos, and atan, with a variety of positive and negative numbers until you are comfortable "thinking" in radians.  Predict the results before you press 'Enter'.

The program rightss (which stands for "right-triangle-side-side") solves a right triangle when the two sides are known.  It uses the atan function in line 2 of section 30.  Notice that the output of the atan function, which is in radians, is converted to degrees by multiplying it by 180/π.

If you understand how rightss works, write one called righths (for right-triangle-hypotenuse-side) which solves a right triangle when the hypotenuse and one side are known.
 

------ marker ------ beginning of working program ------ try it out ------

;|  RIGHTSS, short for RIGHT triangle with "Side-Side" known
    Copyright © 1998 Ronald W. Leigh
    Input: two sides of a right triangle
    Output: solution of unknown sides/angles
Variables:
a/b/c  Sides
aa/bb  Angles                           |;

;10====PROGRAM SETUP

(defun c:rightss ()
(setq pi 3.1415926535897932385)

;20====INPUT

(princ "\nEnter two sides (not hypotenuse).")
(initget 7)
(setq a (getreal "\nLength of one side: "))
(initget 7)
(setq b (getreal "\nLength of other side: "))

;30====CALCULATE & REPORT

(setq c (sqrt (+ (* a a) (* b b))))
(setq aa (* (/ 180 pi) (atan a b)))
(setq bb (- 90 aa))
(princ (strcat
  "\n  Hypotenuse is " (rtos c)))
(princ (strcat
  "\n  Angle " (rtos aa 2 4) "° is opposite side " (rtos a 2 4)))
(princ (strcat
  "\n  Angle " (rtos bb 2 4) "° is opposite side " (rtos b 2 4)))

(princ)
)

-------- marker -------- end of working program -------- try it out --------
 

The program rightsa (which stands for "right-triangle-side-angle") solves a right triangle when the one side and one angle are known.  It uses the sin function at the beginning of section 30.  Notice that the angle entered by the user (in degrees) is converted to radians by multiplying it by π/180 before it is submitted to the sin function.

The initget and getkword functions in section 20 are explained in a later lesson.

If you understand how rightsa works, write one called rightha (for right-triangle-hypotenuse-angle) which solves a right triangle when the hypotenuse and one angle are known.
 

------ marker ------ beginning of working program ------ try it out ------

;|  RIGHTSA, short for RIGHT triangle with "Side-Angle" known
    Copyright © 1998 Ronald W. Leigh
    Input: side and angle of a right triangle
    Output: solution of unknown sides/angles
Variables:
a/b/c  Sides
aa/bb  Angles                           |;
ang    Temporary angle
loc    Location of angle

;10====PROGRAM SETUP

(defun c:rightsa ()
(setq pi 3.1415926535897932385)

;20====INPUT

(princ "\nEnter a side (not hypotenuse) and an angle.")
(initget 7)
(setq a (getreal "\nLength of side: "))
(initget 7)
(setq ang (getreal "\nSize of angle in degrees: "))
(initget "Opposite Adjacent")
(setq loc (getkword "\nIs angle Opposite side or Adjacent to side? (O/A): "))
(if (= loc "Opposite")
  (setq aa ang bb (- 90 aa))
  (setq bb ang aa (- 90 bb))
)

;30====CALCULATE & REPORT

(setq c (/ a (sin (* aa (/ pi 180)))))
(setq b (sqrt (- (* c c) (* a a))))
(princ (strcat
  "\n  Hypotenuse is " (rtos c)))
(princ (strcat
  "\n  Angle " (rtos aa 2 4) "° is opposite side " (rtos a 2 4)))
(princ (strcat
  "\n  Angle " (rtos bb 2 4) "° is opposite side " (rtos b 2 4)))

(princ)
)

-------- marker -------- end of working program -------- try it out --------
 

Holes are often found in a circular pattern, and if you are using coordinate (X-Y) dimensions, one of the cleanest ways to dimension them is with a table of X and Y dimensions placed somewhere near the hole pattern.  This program is called bctable, which is short for bolt circle table.  It creates a table of coordinate (X-Y) dimensions for equally spaced holes on a bolt circle, and illustrates the use of the sin and cos functions.  Several aspects of this program call for explanation.

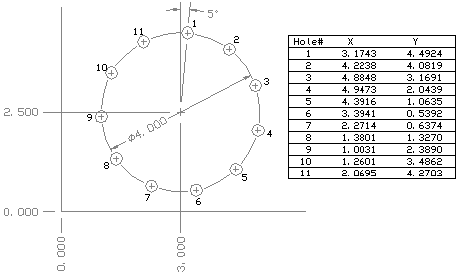
The value of pi -- section 10

AutoLISP presets the variable pi to 3.14159 . . . .   However, pi can be accidentally reset to any other value, so there is no guarantee that pi holds its intended value when your program needs it.  So, whenever you write a program that depends on pi, set it at the beginning of the program.  The value used in the program is accurate to 20 significant digits.

Mono spaced text with variable height -- section 10

In order to make the columns of numbers line up properly, the current text style must use a mono spaced font.  The style must also a variable height (set to zero).  A more sophisticated program would check the current text style, and if needed, create a text style that meets these requirements.  But that would make the program more complex than we would like at this stage in the lessons.  So a simple message is displayed telling the user what is needed.
 

Holes numbered -- sections 20 and 40

The holes are numbered starting at the top and moving clockwise.  At the end of section 20 the user indicates whether or not he/she wants hole numbers placed near the holes.  Then in lines 6 - 8 of section 40, the numbers are arbitrarily placed a certain distance outside the circle (15% of the radius).  This is a quick and simple placement, and the numbers will have to be moved any many cases.  To place them more precisely would require additional input regarding the size of the holes and even then individual numbers would often need to be moved because of other geometry or dimensions.  So this simpler procedure is used.  By the way, an easy procedure for moving all numbers in or out a small distance is to pick them all then scale them around the center of the bolt circle.

Repeat statements -- section 40

Section 40 contains nested iteration loops.  In other words, it has one large repeat statement which includes several nested repeat statements.  All the lines in the larger repeat statement are executed once for each hole.  Notice that the repeat function's first argument is variable num.  Also, each time the loop is executed, the program must know which number hole it is working on, and where that hole is located around the bolt circle.  That is why a counter (variable cnt) is initialized at zero just before the repeat statement is entered, and is incremented by one with each iteration (second line inside the loop).

The smaller, nested repeat statements are used to add spaces at the beginning of the dimension numbers so they will line up vertically in the table.

More is explained about iteration in a later lesson.
 

------ marker ------ beginning of working program ------ try it out ------

;|  BCTABLE, short for Bolt Circle TABLE
    Copyright © 1998 Ronald W. Leigh
    Input: Bolt circle center & diameter,
     Number of holes, Angle offset, dimension offset
     Location of table, height of text in table
    Output: A table of X-Y dimensions for each hole
Variables:

ang     Angle for each successive hole
angoff  Angle offset
anginc  Angular increment between holes
bccen   Bolt circle center
bcdia   Bolt circle diameter
cnt     Counter
dimori  Dimension origin
hn      Hole number as string
hnpref  Hole number preference ("Yes" or "No")
llen    Line length
num     Number of holes
rad     Radius
sp      Start point for successive lines & text
txthei  Text height
ul      Upper left corner of table
xadd    X added distance from origin
xdim    X dimension for hole
yadd    Y added distance from origin
ydim    Y dimension for hole                  |;

;10====PROGRAM SETUP

(defun c:bctable (/ ang angoff anginc bccen bcdia cnt dimori
          hn hnpref llen num rad sp txthei ul xadd xdim yadd ydim)
(setq pi 3.1415926535897932385)
(setq obm (getvar "blipmode") oom (getvar "osmode"))
(princ "\n** Current text style should use one of the following fonts,")
(princ "\n** Monotxt or Monospac821BT, with variable (zero) height.")

;20====INPUT

(initget 1)
(setq dimori (getpoint "\nLocate dimensioning origin: "))

(initget 1)
(setq bccen (getpoint "\nLocate center of bolt circle: "))
(setq xadd (- (car bccen) (car dimori)))
(setq yadd (- (cadr bccen) (cadr dimori)))

(initget 7)
(setq bcdia (getreal "\nDiameter of bolt circle: "))
(setq rad (/ bcdia 2))

(initget 7)
(setq num (getint "\nNumber of equally spaced holes: "))
(setq anginc (/ (* 2 pi) num))

(initget 4)
(setq angoff (getreal "\nClockwise angle offset of hole 1 from vert. <0>: "))
(if (null angoff) (setq angoff 0.0))
(setq angoff (* angoff (/ pi 180)))

(initget 1)
(setq ul (getpoint "\nUpper left corner of table: "))

(initget 7)
(setq txthei (getreal "\nText height: "))
(setq sp ul llen (* txthei 28))

(initget "Yes No")
(setq hnpref (getkword "\nPlace hole numbers near holes? (Y/N) <Y>: "))
(if (null hnpref) (setq hnpref "Yes"))

;30====DRAW TABLE HEADER

(setvar "osmode" 0)
(setvar "blipmode" 0)
(setvar "cmdecho" 0)
(command ".line" sp (polar sp 0 llen) "")
(setq sp (polar sp (* pi 1.5) txthei))
(command ".text" "ML" sp txthei 0 " Hole#    X          Y")
(setq sp (polar sp (* pi 1.5) txthei))
(command ".line" sp (polar sp 0 llen) "")

;40====DRAW TABLE ENTRIES & HOLE NUM'S, VERTICAL LINES

(setq cnt 0)
(repeat num
  (setq ang (+ angoff (* cnt anginc)))
  (setq cnt (1+ cnt))
  (setq hn (itoa cnt))
  (if (= hnpref "Yes")
    (command ".text" "M"
      (polar bccen (- (/ pi 2) ang) (* 1.15 rad)) txthei 0 hn))
  (repeat (- 4 (strlen hn)) (setq hn (strcat " " hn)))
  (setq xdim (* rad (sin ang)) ydim (* rad (cos ang)))
  (setq xdim (+ xadd xdim) ydim (+ yadd ydim))
  (setq xdim (rtos xdim 2 4) ydim (rtos ydim 2 4))
  (repeat (- 11 (strlen xdim)) (setq xdim (strcat " " xdim)))
  (repeat (- 11 (strlen ydim)) (setq ydim (strcat " " ydim)))
  (setq sp (polar sp (* pi 1.5) txthei))
  (command ".text" "ML" sp txthei 0 (strcat hn xdim ydim))
  (setq sp (polar sp (* pi 1.5) txthei))
  (command ".line" sp (polar sp 0 llen) "")
)

(command ".line" ul sp "")
(command ".line" (polar ul 0 llen) (polar sp 0 llen) "")

;====RESET

(setvar "blipmode" obm)
(setvar "osmode" oom)
(setvar "cmdecho" 1)
(princ)
)

-------- marker -------- end of working program -------- try it out --------