Lesson 15
Miscellaneous

This lesson covers certain practical aspects of AutoLISP programming not included in earlier lessons.  Most of the sample programs given in those lessons could be enhanced by incorporating some of these features.

Defaults for quicker, safer data entry

When your program offers a default response, the user has the option of simply pressing 'Enter' to accept the default, or entering something different.  This ability to "click through" one or more defaults has the obvious advantage of speed, but it also allows fewer opportunities for the user to make an error typing the response.

Below are several sample programs, each containing a different type of default.  The programs are basically "do nothing" programs, although they do display the value that was either entered or accepted.

Sample 1: Constant number default

A constant default is always the same, no matter what the user entered the last time the program was run.  It represents what the programmer considers a reasonable response in most cases.  In line 3 of this sample, the user is prompted to enter the length and is given 4.00 as the default.  If the user gives a null response (merely hits 'Enter'), then the getreal function returns nil, which is assigned to len.  Line 4 detects this and assigns 4.0 to len.

(defun c:sample1 (/ len)
(initget 6)
(setq len (getreal "\nEnter length <4.00>: "))
(if (null len) (setq len 4.0))
(princ "\nVariable len is set to: ") (princ len) (princ))

Sample 2: Constant word default

This is also a sample of a constant default.  It allows the user to enter either "S," "M," or "L" and always prompts "M."

(defun c:sample2 (/ size)
(initget "Small Medium Large")
(setq size (getkword "\nSize: Small/Medium/Large <M>: "))
(if (null size) (setq size "Medium"))
(princ "\nVariable size is set to: ") (princ size) (princ))

Sample 3: Variable number default

This is a sample of a variable default, that is, the default that is displayed depends on what the user entered the last time the program was run.  In line 4 this sample uses the variable temp to hold a temporary value, which is evaluated in line 5.  Notice also that the variable len has to be initialized (see line 2) so that, the first time the program is run, it will have a value to be converted and displayed in the prompt (see line 4).  The variable len must be a global variable in order to retain its value after the program is finished executing, so it is not included in the variable list in line 1 (compare Sample 1).

(defun c:sample3 (/ temp)
(if (null len) (setq len 1.0))
(initget 6)
(setq temp (getreal (strcat "\nEnter length <" (rtos len 2 3) ">: ")))
(if temp (setq len temp))
(princ "\nVariable len is set to: ") (princ len) (princ))

The sample program at the end of this lesson, ba2, illustrates the use of variable default prompts.

Samples 4 and 5: Limited response and a number default

Since the initget and getkword functions work with numbers as well as words, they can be used to limit numeric input to certain values.  However, since getkword returns a string, you must remember to convert it.  The example below limits the user's response to any quarter of an inch between one and two inches inclusive, and offers 1.75 as a constant default.

(defun c:sample4 (/ size)
(initget "1 1.25 1.5 1.75 2")
(setq size (getkword "\nSize (1 1.25 1.5 1.75 2) <1.75>: "))
(if (null size) (setq size "1.75"))
(setq size (atof size))
(princ "\nVariable size is set to: ") (princ size) (princ))

But sample4 has a serious drawback.  If the user enters 1.50 or 1.500 instead of 1.5 (the exact string called for in the initget function), getkword will reject it.  Rather than attempting to list all possibilities (which could easily triple the length of the argument to initget), we need to adopt a different approach.

In sample5, below, the user's response is treated as a number rather than a string, which allows, for example, 1.50, 1.500, and 1.5000 to be accepted as equivalent to 1.5.  Also, the default is a variable default using a global variable.

Notice the use of the member function, which tests to see if its first argument (the number entered by the user) is a member of the second argument (the list of numbers).

Also notice the use of the not function, which (1) makes the while test return T when the user enters a number that is not in the list, and thus repeats the prompt, and (2) makes the while test return nil when the user enters a number that is in the list, and thus drops out of the while loop.

Also notice that nil is included in the list of accepted numbers, which allows the user to hit 'Enter' to accept the displayed default.

(defun c:sample5 (/ temp)
(if (null size) (setq size 1.75))
(while (not (member (setq temp
  (getreal (strcat "\nSize (1 1.25 1.5 1.75 2) <" (rtos size 2 3) ">: ")))
  (list nil 1.00 1.25 1.50 1.75 2.00))))
(if temp (setq size temp))
(princ "\nVariable size is set to: ") (princ size) (princ))
 


Writing your own error routine

AutoLISP has a built-in error routine which executes whenever an error occurs.  You can think of this built-in error routine as being named *error* even though, strictly speaking, that it not exactly true.

Here are a few sample expressions and the error messages they produce.  The part of the error message after the word "error:" is called the error string.
 

Expression Error message Reason
(/ 5 0) error: divide by zero Dividing by zero is indeterminate 
and therefore not allowed
(setg var 4.75) error: null function The setq function is misspelled
(setq width .875) error: invalid dotted pair The fraction needs a leading zero (0.875)
(+ 5.0 8.0 "twelve") error: bad argument type Cannot add a string
(sqrt -9) error: function undefined 
for argument 		 Cannot deal with imaginary numbers 
(square roots of negative numbers)
[user presses the 
'Escape' key]		 error: Function cancelled User hit 'Escape' while the program 
was running

When an error occurs, AutoLISP both displays an error message, and dumps the offending expression to screen.  If that offending expression is nested inside another expression in the program, the surrounding expression is also dumped to screen, along with any additional surrounding expressions.  The program is not dumped to screen with the expressions in the same order as they appear in the program file.  Instead, the listing begins with the offending expression, then its surrounding expression, then the next surrounding expression, etc.  This helps you locate the offending code in a long program where the same expression might occur several times, and is referred to as a traceback.

The built-in error routine (*error*) is "tripped" in two ways:

(1) by errors in the program itself, such as those illustrated in the table above (or by programming oversights which allow users to enter bogus input which in turn causes errors), and
(2) by the user hitting the 'Escape' key while the program is running.  In this case, the error message reads: "error: Function cancelled" (note the spelling, especially the capital "F")

The fact that AutoLISP treats an escape as an error, along with the fact that the built-in error routine dumps code to screen, makes it advisable to program your own error routine and set it up to execute instead of the built-in error routine.  Your own error routine can be written in such a way that it allows the user to quit a program by hitting 'Escape', and avoid both the display of an error message and the dumped code, but still reports other errors.

Another reason why it is advisable to define your own error routine is that you will need to use it to reset any system variables that your program changed.  This is explained below under the heading "Saving and restoring system variables."

Whenever a user-defined error routine exists, the built in error routine calls that user-defined error routine and passes it a string argument.  The string is a short phrase describing the error, such as the phrases after "error:" in the table above.  The user-defined error routine must have one variable in its variable list to accept that string (see the variable str in the two sections below).  Of course, the remainder of the user-defined error routine can do whatever it wants (including nothing) with that string.

One way to write an error routine -- not recommended

This approach to placing error routines in your programs works, but it is not recommended.  It is included here only to help you understand user-defined error routines a little better.

Suppose that, at the beginning of a particular program called program1, you defined an error routine using the name *error*.  In other words, your program might look something like this:

When program1 is run, the first thing it does is to define (stores in memory) the *error* program so that it is waiting to be called if an error occurs.  Then, if no error occurs, the last thing the program does is to set *error* to nil, which means that future errors will trip the built in error routine.  However, if an error occurs while this program is running (or the user hits 'Escape'), then the user-defined error routing will execute.  The message "***ERROR***XXXXXXX*** will be displayed (where XXXXXXX is the error string passed by the built-in error routine), and no traceback will occur.

The disadvantage of this approach is that it requires an error definition in every program.  It does not allow for an external error routine to be written and then used by various programs, as the following section explains.

A better way to write an error routine

Again, suppose you want to have a user-defined error routine for a program called program1.  This time, however, we will define it outside of program1.  It could be in the same file, or in a different file.  If it is in the same file, it might look like this:

In this approach, the error routine is defined under a name different than *error*.  The name might include the program name, as it does above, or it might include a more general name if it is being written for several closely related programs.

The user-defined error routine becomes effective when it is assigned to *error* by the setq function (see line 2 of PROGRAM1 above).  But immediately before this, the built-in error routine is "captured" and placed in variable olderr.

If no error occurs, the last thing program1 does is to re-enable the built-in error routine by retrieving it from variable olderr and assigning it back to *error*.  However, if an error occurs while this program is running (or the user hits 'Escape'), then the user-defined error routine will execute.  The message "***ERROR***XXXXXXX*** will be displayed (where XXXXXXX is the error string passed by the built-in error routine), and no traceback will occur.

The advantage of this approach is that one user-defined error routine can be written and used by various programs.  It is probably safest to do this (write one error routine for several programs) if all the programs will be defined in the same file and the error routine also defined in that file.  This guarantees that the error routine will be loaded when the programs are loaded, and thus be available in memory.

The sample program below, ba2, illustrates the use of an error routine similar to the one above.

By the way, if your program changes any system variables, it is also wise to restore those system variables to their original settings both at the end of the program and (in case an error occurs) at the end of the error routine.  Two procedures for accomplishing this are explained in the next section.

Saving and restoring system variables

Your program will often set certain system variables.  For example, if the program draws entities on screen, you will want to turn BLIPMODE off so the drawing looks clean without the need for a redraw.  Or, more importantly, you will want to turn all running osnap modes off.  If you don't, you program might attempt to place an entity at a certain calculated location but the running osnap mode might move it somewhere else!

Of course, your program should capture and store the user's current settings for any system variables that it intends to change, so it can restore the user's settings when the program is done.

If there are just a few system variables, it is sufficient to use a straightforward approach in which you retrieve the user's settings with the getvar function and save them in certain variables, then restore them with the setvar function at the end of the program.  Here is an example of this approach in which blipmode and running osnap modes are saved in variables obm (for "original blip mode") and oom (for "original osnap mode"):

Remember that, besides resetting the system variables at the end of the program, they should also be reset in your error routine.  If an error occurs (or if the user hits 'Escape'), the end of your program will never be executed, but the error routine will.  So the error routine will have to do the resetting.

The above procedure works fine if there are only a few system variables to be saved and restored.  However, in some more complex programs, you may find that you need to save and restore as many as 20 - 40 system variables.  When this is the case, you do not want to use the above procedure, because it involves making sure that you have the same set of variables in three separate places -- at the beginning of the program, at the end of the program, and in the error routine.

Here is a better approach when you have lots of system variables to save and restore.  Build a list of system variables at the beginning of the program and save it in a variable called svlist.  Then use svlist to capture the user's settings and to restore those settings both at the end of the program and in the error routine.  This will permit you to maintain only one list of system variables.

The first line above simply builds a list of the names of the system variables.  The next two lines add the current settings to those names and produce a list that looks something like this:

        (("blipmode" . 1) ("osmode" . 3) . . . )

This is the form of svlist that is used at the end of the program and in the error routine to restore the users original values.

Placing an AutoLISP program in a pull down menu

Even though these lessons are not intended to cover menu customization, you will find it extremely handy to place AutoLISP programs in pull down menus.  So we will look at one example here.

In order to have something specific to illustrate, lets assume that you have a program called incap which you would like to appear in the "Insert" pull down menu.  This program inserts a cap screw in an assembly drawing.  It asks for certain specifications (type, size, view, etc.), creates a block, then allows the user to place the block in the drawing.  After you have written the program, you can place it in the pull down menu by following the steps below.

By the way, if you have created a lot of custom toolbars, you many not want to edit the acad.mnu file directly.  Instead, you could make a copy of the acad.mnu file and give it a different name such as acad1.mnu.  In the following discussion, we will assume that you are editing the acad.mnu file.

Step 1

Edit the INSERT section of the pull down menu in the menu file.  The INSERT section is listed under the heading "***POP4".  You will add this line -- [Cap Screw]^C^C(incap) -- as shown in line 5 below, and save the file.  Of course, you can define your program either as a function or an AutoCAD command.  Below we are illustrating it as though it is defined as a function.

Step 2

In order to test your altered menu file, reload it using the MENU command.  When you reload it, request the .mnu file (acad.mnu) so that it will be recompiled.  After it is recompiled and loaded, you new entry "Cap Screw" should appear in the pull down.  However, if you pick it now, it may not work.  You must make sure that your AutoLISP program (incap) is loaded first.  Once incap is loaded, you should be able to call it from the menu.

Step 3

If you want your incap program to load automatically, you can do one of two things.  (1) Either place the incap program in the acad.mnl file.  Or (2) expand your addition to the acad.mnu file so it looks like this:

         [Cap Screw]^C^C^P(if (null incap) (load "C:/xxxx/incap"))^P(incap)

The if statement tests to see if incap is nil (undefined in memory), in which case it loads it before attempting to run it.  Obviously, your menu file must know what folder this program is located in.
 


Finding intersections of existing geometry

Sometimes your program may need to find a single intersection of two straight lines.  Other times it may need to let the user select one of several possible intersections between a circle and an arc, or between a spline and an ellipse.  Sometimes your program will already have created the entities that intersect, other times the entities will have been created directly by the user or by a different program.  Sometimes your program needs input from the user, other times it needs to operate automatically.  With all these different situations, and all the different types of geometry that can intersect, there are dozens of possible scenarios which you may encounter in your programming.

Four sample scenarios are covered below.  The fourth sample is the most general in that it can be used with all combinations of lines, circles, arcs, ellipses, portions of ellipses, splines (open and closed), etc., but it does require user input.

All four samples pertain to 2D intersections.

Scenario 1

Two straight lines already exist in the drawing (they are not created by this program).  The user will select two lines.  This program returns the intersection point.

Scenario 2

Your program has created two straight lines.  Since the program already knows the coordinates of the endpoints of both lines, it can simply supply those coordinates to the inters function to find the intersection point.  For example, if the endpoints for the first line are in variables a and b, and the endpoints for the second line are in variables c and d, then one of the following two sample lines could be used to return the intersection point.  (See inters function.)

Scenario 3

Your program creates two circles, so it knows the circles' locations and sizes.  You want your program to automatically indicate the two intersection points without any additional input from the user.

In section 30, the program checks to see if the two circles actually intersect.  In section 40, the program uses the following equations (based on the diagram below and the Pythagorean theorem) to calculate the intersection points.

    rad12 - travel2  =  throw2  =  rad22 - (dist - travel)2

    Solving for travel:     travel  =  (rad12 - rad22 + dist2) / 2 dist

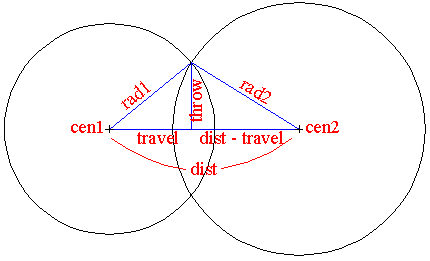
Trig for circles in inters3
If the circles already existed (they were not created by your program) and the user has to pick the two circles, you could use a technique similar to the one illustrated in Scenario 1 above.  (In the entity list for a circle, the center is associated with code 10 and the radius with code 40.)

Scenario 4

Perhaps your program has created two or more intersecting entities, or perhaps they were created by another program or "manually" by the user.  In any of these cases, you may want the user to select the exact intersection point on screen rather than selecting the entities that intersect.  This is the preferred method when entities intersect in two or more places, or when there are multiple entities intersecting in many places.

First, the program prompts the user to select the intersection point.  (As you move the cursor around a crowded screen, you will see that all intersections are shown as the cursor approaches them.)  Then the program runs the ID command with the "intersect" osnap mode.  Then it retrieves the point from system variable "LASTPOINT" by use of getvar function and saves it in variable ipoint.  This method works with any combination of lines, arcs, circles, ellipses, splines, etc.

If you want the user to be able to select from actual intersections, use the "int" osnap mode with the ID command as shown above.  If you want the user to be able to select from apparent intersections (resulting from extending the entities) use "appint" instead.

Manipulating DOS directories and programs

Manipulating DOS directories is done the same as it was done in earlier versions of AutoCAD.  You use the SHELL command inside the AutoLISP command function.  Here are three examples:
 

Example 1:    (command "shell" "DIR>LIST")
Shells out of AutoCAD, then runs the DIR command and uses the redirection symbol to send the output to a file called LIST.
Example 2:    (command "shell" "MD C:\\WORK\\SUB1")
Shells out of AutoCAD, then makes a directory with the path C:\WORK\SUB1
Example 3:    (command "shell" "EDIT FILE1")
Shells out of AutoCAD, then runs the text editor called EDIT and opens the file called FILE1


A few sample subroutines

One of the most common conversions needed in AutoLISP programming is to convert radians to degrees and vice versa.  If your program needs to make such a conversion in only one or two places, then it is simplest to program the conversion at that location in the program.  However, if your program has to make such a conversion many times, then it is more efficient to define a short conversion program that can be called from anywhere in the program.  You might want to place it in the same file as the main program so it will be sure to be loaded and available.  The same approach holds true for many other subroutines.

Below are just a few sample subroutines that you might find helpful.  Many serious programmers build their own "library" of subroutines.  You can use these few examples to get started.

1.  Converting radians to degrees:

    (defun rtd (r) (* r (/ 180 pi)))

2.  Converting degrees to radians:

    (defun dtr (d) (* d (/ pi 180)))

3.  Finding the tangent of an angle:

    (defun tan (a) (/ (sin a) (cos a)))

4.  Finding the arc sine of a ratio:

        See Lesson 7, Defining your own arc sine and arc cosine functions.

5.  Finding the arc cosine of a ratio:

        See Lesson 7, Defining your own arc sine and arc cosine functions.

6.  Rounding a number to a certain increment:

    (defun round (num inc) (* (fix (+ (/ num (float inc)) 0.5)) inc))


Sample program, ba2

This program, ba2, is an enhanced version of the ba (bend allowance) program from Lesson 3.  It includes two added features, namely, default prompts and an error routine.

Default prompts

This program gets three inputs from the user, namely, the material thickness, the inside radius, and the bend angle.

Since many bends are 90 degree bends, the input section for the bend angle (section 70) uses a constant default of 90 degrees.

However, the input sections for the thickness (section 50) and radius (section 60) both use a variable default, which displays the user's previous input as the default.  Notice that the names of these two variables have been expanded to include the name of the program (the old variable name thick became ba2thick, and irad became ba2irad) and that both of these variables are now global.  (They must be global so they will retain their values from one use of the program to the next.)  They are marked "GLOBAL" in the documentation at the beginning of the program to remind the programmer not to include them in the list of variables in section 40.  Also, their names have been expanded to avoid conflict with similarly named global variables from other programs that might be run before ba2 is run again.

Both of the variables ba2thick and ba2irad are initialized for two reasons.  First, when the program is run for the first time, these variables should contain reasonable values to be displayed in the prompts.  Second, if they were not initialized, they might (at best) contain reals that are unreasonably out of range for this program, or (at worst) contain some other data type, such as a string, which would cause the rtos function to crash.  The most likely problem, of course, is that these variables would simply be nil, which would also cause the rtos function to crash.

Error routine

The error routine is based on the ideas described above under the heading "Writing your own error routine."
 

------ marker ------ beginning of working program ------ try it out ------

;|  BA2, short for Bend Allowance, 2nd version
    Copyright © 1988, 1999, Ronald W. Leigh
    Input: Material thickness, inside radius, angle
    Output: Developed length of neutral arc
Variables:
ang       Angle
ba2irad   Inside radius, GLOBAL
ba2thick  Material thickness, GLOBAL
frac      Fraction of thickness, from irad to neutral arc
lona      Length of neutral arc
temp      Temporarily holds input, sections 50 & 60     |;

;20====ERROR ROUTINE

(defun ba2error (str)
(if (/= str "Function cancelled")
  (princ (strcat "\n***ERROR***" str "***")))
(setq *error* olderr)
(princ)
)

;40====PROGRAM, SETUP

(defun c:ba2 (/ ang frac lona temp)
(setq olderr *error* *error* ba2error)

;50====Get thickness, Use previous thickness (or .125) as default

(if (null ba2thick) (setq ba2thick 0.125))
(initget 6)
(setq temp (getreal (strcat "\nMaterial thickness <" (rtos ba2thick 2 3) ">: ")))
(if temp (setq ba2thick temp))

;60====Get radius, Use previous radius (or 1.0) as default

(if (null ba2irad) (setq ba2irad 1.0))
(initget 4)
(setq temp (getreal (strcat "\nInside radius <" (rtos ba2irad 2 3) ">: ")))
(if temp (setq ba2irad temp))

;70====Get angle, Use constant default of 90

(initget 6)
(setq ang (getreal "\nAngle <90>: "))
(if (null ang) (setq ang 90))

;80====Calculate frac & lona, Report bend allowance

(setq frac (+ (/ ba2irad ba2thick 16) 0.25))
(if (> frac 0.5) (setq frac 0.5))
(setq lona (/ (* pi ang (+ ba2irad (* frac ba2thick))) 180))
(princ "\nBend allowance = ")
(princ lona)

;90====RESET

(setq *error* olderr)
(princ)
)

-------- marker -------- end of working program -------- try it out --------
 


HOME

Copyright © 1988, 1998 Ronald W. Leigh